"Para mí no hay emoción o satisfacción comparable a la que produce la actividad creadora, tanto en ciencia como en el arte, literatura u otras ocupaciones del intelecto humano". Esta acertada frase de Severo Ochoa podría decirse que intenta resumir el espíritu de este blog, aunque... no nos engañemos; al final todo esto se va a convertir en un amistoso pero intenso campo de batalla en el cual habrá que elegir ser de Kas Naranja o de Kas Limón. Y eso, nos mola. Así pues, me dejo ya de rollos porque ahora es mi turno y os hablaré de ciencia.
¿Se puede explicar todo con números?
Existe un número que es especial, diferente, bastante peculiar... que se presenta espontáneamente en la naturaleza y en nuestro día a día, y que, en caso de no conocerlo, consigue ocultarse de manera impecable de nuestra razón: el número perfecto. Dicha cifra se conoce como el número áureo, divina proporción o número phi, en honor a Fidias, el arquitecto del Partenón.
Ahora bien... ¿de dónde sale ese número? ¿Cuál es exactamente esa proporción digna de dioses?
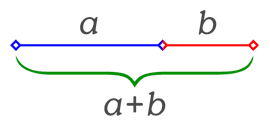
Supongamos que tenemos un segmento de longitud total a+b. Ahora lo dividimos en dos segmentos, tal que la proporción a+b/a sea igual que a/b. Por tanto, tenemos la siguiente ecuación:

Podemos designar arbitrariamente que b=1 por simplificar y que a=x, por lo que obtenemos una ecuación de segundo grado que espero que todos (sí sí, los de letras también...) sepáis resolver.

Las dos soluciones son


Obviamente, desechamos la segunda porque una longitud negativa no tiene sentido. Es como tener un lápiz que mide -10cm. Absurdo, ¿verdad? La primera solución es el famoso número de oro. Bueno....¿y qué? Aplausos y pa' casa, ¿no? Pues NO. El número áureo tiene mucha más miga de lo que parece. Lo de arriba ha sido tan sólo una cutre demostración.
Por ejemplo, (¡sencillo, directo y al alcance de todos!) estira el brazo y mide desde el hombro hasta la punta de tus dedos y el resultado que obtengas divídelo entre la distancia que hay desde el codo hasta de nuevo la punta de los dedos. El resultado debería sonarte. El mismo procedimiento también es aplicable a la distancia cadera-pies/rodilla-pies y a la de cabeza-pies/ombligo-pies. Todo ello queda reflejado en "El Hombre de Vitrubio" de Da Vinci.

Por tanto, si eres más feo/a que un orco de Mordor y eso te preocupa... tranquilo/a, siempre podrás consolarte pensando que eres matemáticamente perfecto/a. (¡Conmigo funciona!)
Por otro lado, la sucesión de Fibonacci (si habéis leído "El Código da Vinci" os sonará de algo) también oculta el número de oro entre sus términos. Para los que no la conozcáis, esta serie empieza en 0 y se forma sumando a un término, el término anterior. Es decir: 0,1,1,2,3,5,8,13,21,34,55,89,144... etc. Dividamos un término por el anterior...
5/3=1.666667
8/5=1.6
13/8=1.625
55/34=1.617647
144/89=1.617977
2584/1597=1.6180338... que es aproximadamente phi.
Por tanto, la sucesión de Fibonacci, sin quererlo ni pretenderlo, porta una belleza intrínseca que puede ser utilizada para construir aquello que denominamos como "rectángulos áureos": rectángulos perfectos y que todo el mundo tiene en mente cuando pensamos en los susodichos. Ni demasiado anchos ni demasiado largos. Vamos... aplicando la filosofía de Platón vendría a ser algo parecido a la "idea de rectángulo". Y éstos se construyen de la siguiente forma:


Es decir, se construyen en base a los diferentes términos de Fibonacci (hay más formas de hacerlos, pero esta es la más sencilla) y tienen la propiedad de que el cociente entre sus lados es la divina proporción. A la espiral logarítmica resultante se la conoce como "espiral de durero", que es la trayectoria que siguen, por ejemplo, los halcones cuando acechan a sus presas, así como la forma que tienen los caparazones de ciertos moluscos (el extinguido Ammonites es el más representativo).

De la belleza propia de estos rectángulos se han aprovechado gran cantidad de artistas y arquitectos para darle un toque extra de "perfección" a sus obras. Véase el Partenón o las proporciones de casi cualquier escultura.

Ahora os planteo lo siguiente: pensad en la forma que tiene un DNI, cualquier tarjeta de crédito, un sobre o incluso una cajetilla de tabaco. ¡Qué forma más agradable para la vista tienen esos rectángulos... áureos! A partir de ahora ya no veréis esos objetos cotidianos de la misma forma.
Como dato curioso, el símbolo del pentáculo propio de la secta pitagórica, también esconde esta proporción armoniosa. Dividiendo cualquier diagonal del pentágono que lo envuelve con uno de sus lados, obtenemos el dichoso numerito. Así pues, el símbolo estrellado de dicha secta está formado por lo que se llaman "triángulos áureos". Y para más rebuscamientos, también existe un "ángulo de oro", que es por el que se distribuyen las hojas de ciertas plantas en su crecimiento alrededor del tallo, de tal manera que se quiten la mínima luz posible las unas a las otras.
Como podréis observar, este número se vale de sí mismo para crear una situación estable, de equilibrio, de perfección y armonía a su alrededor. Lo encontramos en la naturaleza, que fluye por sí misma... o bien es dicha constante la que nos encuentra a nosotros, porque somos quienes la utilizamos para desarrollar nuestras obras, nuestro arte, ya sea en escultura, en pintura, en arquitectura o incluso en música. Un claro ejemplo lo encontramos en la manera en la que están organizadas las octavas de un piano. (¡Atención a los números de Fibonacci!)
Pues bien, ¿para qué demonios sirve toda esta parafernalia de números divinos y secciones de 25 kilates? Realmente, y mucho me pesa decirlo, no sirve para "nada"... más bien, no sirve para nada que se le pueda sacar un rendimiento práctico inmediato. En mi opinión, simplemente sirve para darle una nueva visión al mundo en el que vivimos, llena de detalles inapreciables pero que tras conocerlos (como puede ser el saber la existencia del número áureo) reparamos en ellos con gran facilidad y nos arrancan una sonrisa al reconocerlos.
Esta es sólo una muestra de lo que viene a ser "la poesía de las matemáticas" que se mencionaba en el post introductorio: no es necesario darle una aplicación, simplemente hay que sentarse y contemplar su belleza.
"Espero poder haberos transmitido algo de la emoción que un científico siente cuando encuentra algo nuevo, algo que es él el primero en ver. Mi mensaje, dirigido sobre todo a la juventud, es que si sienten inclinación por la ciencia, la sigan, pues no dejará de proporcionarles satisfacciones inigualables".
Dichas palabras de nuevo no son mías sino que se las he vuelto a robar a Severo Ochoa, aunque eso sí, las comparto completamente.
Pues nada, encantado de conoceros y bienvenidos al blog. Espero que os guste.
Si estáis interesados en saber más sobre el número áureo o queréis una explicación alternativa, os recomiendo estos vídeos:
------------------------------------------------------------------------------------------------
Faraday. Escribiendo entre universos.

No hay comentarios:
Publicar un comentario